Pourquoi multiplie-t-on en probabilités lorsqu’il s’agit de calculer la probabilité de l’intersection de deux événements ?

Cette pratique découle de la définition des probabilités conditionnelles.

Définition : Soient 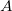et deux événements de l’univers 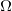, avec 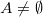. La probabilité que l’événement se réalise sachant que l’événement 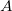a été réalisé est appelée probabilité conditionnelle de sachant 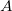, est notée 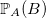et vaut .

Nous allons tenter d’expliquer cette définition a priori peu intuitive et de montrer en quoi elle justifie l’emploi de la multiplication.

Explication : Soient 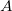et deux événements de l’univers 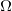, avec 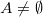. Remarque liminaire : calculer 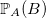revient à calculer 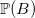dans 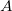, vu comme un nouvel univers correspondant à l’ensemble des issues possibles une fois que 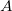a été réalisé.

Par définition de la probabilité, nous avons,

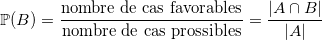
Ainsi,

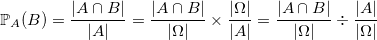Nous avons donc réintroduit 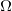et, en remarquant que

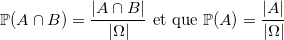nous pouvons en déduire que

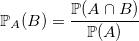Corolaire : De la définition que nous venons d’expliquer, il vient que

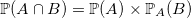ce qui explique que la multiplication soit utilisée pour calculer la probabilité de l’intersection de deux événements.

Par ailleurs, dans le cas où les événements 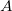et sont indépendants - c’est-à-dire lorsque 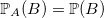-, nous avons

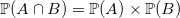Ainsi, la probabilité de l’événement “Obtenir deux fois le nombre 6 lors de deux lancés indépendants d’un dé à six faces non pipé” vaut 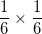et non .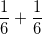