RSA - Attaque des Modules Communs

Parmi les nombreuses attaques side-channel applicables à certaines utilisations maladroites du cryptosystème RSA, l’attaque des modules communs, dont l’existence est rendue possible pas une mauvaise génération de clés, se place parmi les plus simples à mettre en place, mais n’en est pas moins redoutable. Nous allons ici en développer l’idée, et en proposer une implémentation.

Attaque des modules communs

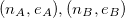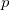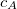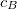Soient deux clés publiques RSA appartenant respectivement à A et B, deux récepteurs, et un message à transmettre, chiffré par un émetteur avec chacune de ces deux clés. Notons et les deux cryptogrammes ainsi obtenus.

Nous avons alors :

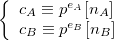
L’attaquant connaît la valeur des clés publiques de A et B, et a intercepté les deux messages chiffrés.

Supposons par ailleurs que les modules des clés sont communs, c’est-à-dire que 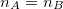(appelons-les ), et que les deux exposants publics sont premiers entre eux, c’est-à-dire que .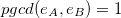

D’après le théorème de Bachet-Bézout,

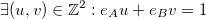
Par conséquent, nous avons :

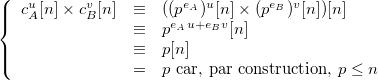
Nous avons donc montré que l’attaquant n’a qu’à calculer le produit 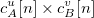pour obtenir le message en clair, sans disposer des clés privées de A et B.

Implémentation

Dans l’implémentation que nous proposons, nous avons pris une précaution qu’il convient de préciser : dans le calcul du produit sur lequel repose l’attaque des modules communs, il est important de noter que les calculs ont lieu dans l’anneau 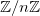, si bien qu’une optimisation conséquente peut être mise en place afin de réduire de manière considérable le temps d’exécution : l’exponentiation modulaire, gérée nativement par le langage python.

Dans l’exemple d’utilisation suivant, deux paires de clés publiques sont instanciées de telle sorte qu’elles ont le même module n, et des exposants premiers entre eux. Un texte est chiffré avec chacune d’elles, et le programme comod.py réalise une attaque par modules communs, dévoilant ainsi le message initial.

# Key generation
>>> p=6468246416824864441327
>>> q=122488752143253143415671
>>> n=p*q
>>> eA=65537
>>> eB=263 # pgcd(eA,eB)=1

# Plaintext

>>> pt=1015285799393168187692228316901635442 # decimal value

# Cipher

>>> cA=pow(pt,eA,n)
>>> cB=pow(pt,eB,n)
>>> cA
40337798257696192889062357882574022113567716
>>> cB
459998051675062019977695880586159168424442224

# Common Modulus Attack
zweisamkeit@linux [ RSHack ] --> ./rshack.py 



        ~~~~~~~~~~~~~~~~~~~~~~~~~
                  RSHack         
               Zweisamkeit       
                GNU GPL v3       
        ~~~~~~~~~~~~~~~~~~~~~~~~~



    List of the available attacks:

        1. Wiener Attack
        2. Hastad Attack
        3. Fermat Attack
        4. Bleichenbacher Attack
        5. Common Modulus Attack
        6. Chosen Plaintext Attack

    List of the available tools:

        7. RSA Public Key parameters extraction
        8. RSA Private Key construction
        9. RSA Ciphertext Decipher
        10. RSA Ciphertext Encipher

    What attack or tool do you want to carry out? 5

             ***** Common Modulus Attack *****

         Arguments [-h] -n common modulus -e1 first exponent -e2 second exponent -c1 first cipher -c2 second cipher:

            -n 792287432151946079584633822001040067951835417 -e1 65537 -e2 263 -c1 40337798257696192889062357882574022113567716 -c2 459998051675062019977695880586159168424442224


        ~~~~~~~~~~~~~~~~~~~~~~~~~
          Common Modulus Attack  
               Zweisamkeit       
            GNU GPL v3 License   
        ~~~~~~~~~~~~~~~~~~~~~~~~~


    [+] Decimal plaintext:  1015285799393168187692228316901635442 

    [+] Interpreted plaintext:  Éternel retour