RSA - Attaque de hastad

La plupart de failles de sécurité relatives aux algorithmes de cryptographie modernes sont dites « side-channel attack », c’est-à-dire dues à des facteurs externes, tels que les implémentations et utilisations qui en sont faites. Nous allons étudier l’Attaque de Hastad, aussi connue sous le nom de « Broadcast Attack », qui profite d’une faille d’utilisation du cryptosystème RSA.

Attaque de Hastad

Soit 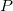un message envoyé en broadcast à 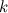personnes, .

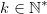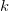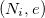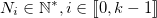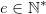Chacune de ces personnes possède une clé publique , avec et l’exposant public invariant dans l’ensemble des clés utilisées.

Soit 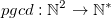la fonction PGCD.

On suppose par ailleurs que :

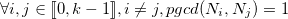
et que :

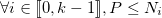
On envoie donc 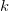fois le message 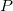chiffré avec chacune des 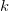clés publiques utilisant toutes comme exposant publique, en supposant de plus que 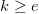. Nous appellerons ces messages .

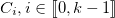Supposons qu’un attaquant ait récupéré l’intégralité de ces messages chiffrés.

En reprenant la procédure de chiffrement de l’algorithme RSA, on obtient le système de congruences suivant :

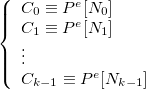
On sait que :

.

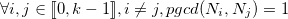Ainsi, d’après le Théorème des Restes Chinois, on a :

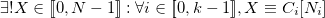, avec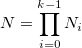

On a de plus :

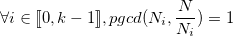, car .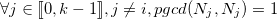

Ainsi, d’après le Théorème de Bachet-Bézout,

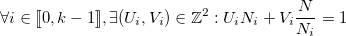
Soit 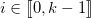. Nous recherchons ici l’inverse modulaire de 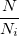modulo 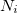, à savoir 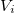dans notre identité de Bézout. Pour ce faire, il suffit d’appliquer l’algorithme d’Euclide étendu à 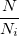et .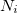

Ainsi, nous obtenons la division euclidienne 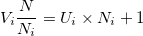. Autrement dit, .

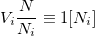Nous avons donc :

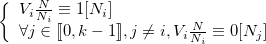
car

.

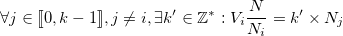Nous pouvons ainsi proposer une solution modulo 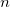au système de congruences obtenu à partir du Théorème des Restes Chinois :

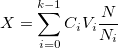
En conséquence, on a .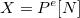

Or, sachant que et que 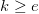, on a .

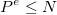Autrement dit, on a .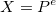

Il nous suffit donc de déterminer la racine -ième de 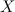pour obtenir le message déchiffré .

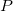Pour résumer, l’Attaque de Hastad permet de casser un chiffrement RSA quelle que soit la taille des clés, sous réserve que l’on ait intercepté le même message chiffré avec différentes clés publiques utilisant toutes le même exposant publique, et que le nombre de messages interceptés soit au moins égal à cet exposant.

Implémentation

Nous avons réalisé deux implémentations de l’attaque de Hastad. La première en Bash, dans le cas particulier où 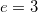(3 étant le seul exposant usuel à être relativement petit, il semble déraisonnable, avec la puissance de calcul d’un ordinateur personnel, de tenter une attaque sur des exposants plus élevés, tels que 65537), et la seconde en python, dont nous recommandons l’utilisation, qui, elle, n’impose aucune contrainte sur l’exposant.

Dans la démonstration suivante, nous avons fait en sorte que le plaintext fasse 256 octets, soit la taille d’un bloc de chiffrement RSA 2048, en le suffixant de nombreux espaces. Ainsi, openssl n’applique pas de padding aléatoire PCKS#1 v1.5, ce qui compromettrait la condition d’égalité stricte entre les messages à chiffrer qui seraient de la forme : 00 02 [ RANDOM PADDING ] 00 [ PLAINTEXT ].

Les clés et les messages ont été générés avec le script gen.sh disponible dans le répertoire Linux.

zweisamkeit@linux [ RSHack ] –> ./rshack.py

    ~~~~~~~~~~~~~~~~~~~~~~~~~
              RSHack         
           Zweisamkeit       
        Licence GNU GPL v3   
    ~~~~~~~~~~~~~~~~~~~~~~~~~



List of the available attacks:


    1. Wiener Attack
    2. Hastad Attack
    3. Fermat Attack
    4. Bleichenbacher Attack
    5. Common Modulus Attack

    6. RSA public key parameters extraction

What attack do you want to carry out? 2

         ***** Hastad Attack *****

    Arguments ([-h] -k0 path_to_key0 -k1 path_to_key1 -k2 path_to_key2 -c0 cipher1 -c1 cipher2 -c2 cipher3): -k0 public0.pem -k1 public1.pem -k2 public2.pem -c0 15[...]23 -c1 16[...]16 -c2 12[...]98


~~~~~~~~~~~~~~~~~~~~~~~~~
      Hastad Attack      
       Zweisamkeit       
    GNU GPL v3 License   
~~~~~~~~~~~~~~~~~~~~~~~~~



Keys paramters extraction...

Modular inverse calculation...
Modular inverse calculation done...

System solution cube calculation...
System solution cube calculation done

System solution calculation...
System solution calculation done

Solution interpretation...
Solution interpretation done

    The plaintext is: Il etait paresseux, a ce que dit l'histoire,
    Il laissait trop secher l'encre dans l'ecritoire.
    Il voulait tout savoir mais il n'a rien connu.
    
         - Gerard de Nerval, Epitaphe