RSA - Attaque de Fermat
La solidité du chiffrement RSA repose sur la difficulté de factoriser le module d’une paire de clés donnée. En effet, il s’agit de retrouver, à partir du module obtenu lors de la création des clés en calculant le produit de deux nombres premiers, dans les faits très grands.
Une méthode naïve pourrait être de chercher l’ensemble des nombres premiers inférieurs à la racine carrée de n, et de tenter de diviser n par chacun de ces nombres de manière dynamique.
Cette méthode est évidemment très complexe : même les tests de primalité probabilistes, tels que celui de Miller - Rabin, ont une complexité polynomiale (voir ces diapositives), bien que relativement efficace. De plus, les divisions successives de grands nombres peuvent s’avérer également très coûteuse.
Le mathématicien Pierre de Fermat a proposé une méthode de factorisation des nombres impairs (en particulier des nombres premiers tels que les modules RSA) qui, dans certain cas, va s’avérer très efficace.
Prérequis
Soit 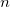 un nombre premier, obtenu en effectuant le produit de deux nombres premiers distincts
un nombre premier, obtenu en effectuant le produit de deux nombres premiers distincts 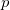 et
et 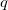 .
.
Nous avons alors :
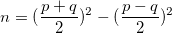
En effet,
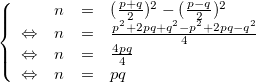 .
.
Autrement dit, 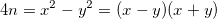 , avec
, avec 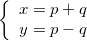 .
.
Par ailleurs, nous remarquons que 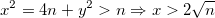 .
.
En effet, par construction de 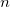 ,
, 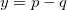 est non-nul.
est non-nul.
Afin de factoriser 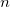 , nous devons donc trouver deux entier
, nous devons donc trouver deux entier  et
et 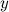 tels que
tels que 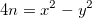 .
.
Méthode de Fermat
Partant de ces observation, Fermat propose l’algorithme suivant :
- Posons
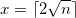 , la première valeur de
, la première valeur de  possible ;
possible ; - Tant que
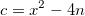 n’est pas un carré parfait, nous incrémentons
n’est pas un carré parfait, nous incrémentons  de 1;
de 1; - Une fois que nous avons trouvé
 tel que
tel que 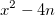 est un carré parfait, nous avons la décomposition de
est un carré parfait, nous avons la décomposition de 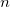 en une différence de carrés :
en une différence de carrés : 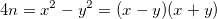 ;
; - Par identification, nous avons retrouvé les facteurs premiers de n :
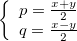 .
.
Optimisation
Notons  la valeur de x à l’itération
la valeur de x à l’itération 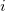 appartenant à
appartenant à 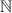 .
.
Nous avons donc, à l’itération 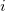 ,
, 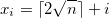 .
.
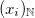 est une suite arithmétique de raison 1, si bien que nous obtenons la relation de récurrence suivante :
est une suite arithmétique de raison 1, si bien que nous obtenons la relation de récurrence suivante :
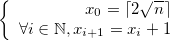
Ainsi, nous avons, 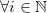 :
:
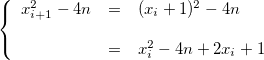
Ainsi, à l’itération 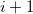 , il ne sera pas nécessaire de calculer le carré de
, il ne sera pas nécessaire de calculer le carré de 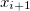 . En effet, il nous suffira de reprendre la valeur de
. En effet, il nous suffira de reprendre la valeur de 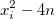 , et de lui ajouter
, et de lui ajouter 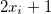 .
.
Nous avons donc remplacé le calcul du carré par de simples sommes.
Implémentation
Dans notre implémentation, nous avons ajouté une fonctionnalité permettant de retrouver l’exposant privé de la paire de clés, ainsi que la reconstruction de la clé privée.
Dans l’exemple suivant, nous avons généré un module 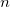 obtenu à partir de nombres premiers
obtenu à partir de nombres premiers 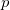 et
et 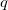 vérifiant la condition
vérifiant la condition 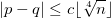 , avec
, avec 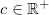 une constante suffisamment petite.
une constante suffisamment petite.
En effet, nous avons 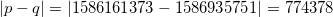 , d’une part, et
, d’une part, et 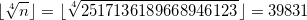 , d’autre part, si bien que
, d’autre part, si bien que 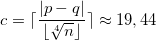 .
.
zweisamkeit@linux [ RSHack ] --> ./rshack.py
~~~~~~~~~~~~~~~~~~~~~~~~~
RSHack
Zweisamkeit
Licence GNU GPL v3
~~~~~~~~~~~~~~~~~~~~~~~~~
List of the available attacks:
1. Wiener Attack
2. Hastad Attack (Linux only)
3. Fermat Attack
4. Bleichenbacher Attack
5. Common Modulus Attack
6. Parameters extraction
What attack do you want to carry out? 3
***** Fermat Attack *****
Arguments ([-h] -n modulus -e exponent): -n 2517136189668946123 -e 65537
~~~~~~~~~~~~~~~~~~~~~~~~~
Fermat Attack
Zweisamkeit
GNU GPL v3 License
~~~~~~~~~~~~~~~~~~~~~~~~~
n factorization: 1586161373 * 1586935751
Private exponent: 629120813201733473
Private key:
-----BEGIN RSA PRIVATE KEY-----
MDoCAQACCCLuqgc0f3DLAgMBAAECCAi7FgvfsbdhAgReiubdAgRelrfHAgQxGkdp
AgQWaJJlAgQc69EW
-----END RSA PRIVATE KEY-----