L’attaque de Bleichenbacher, applicable sur de nombreux protocoles reposant sur l’algorithme de cryptographie asymétrique RSA, permet de décrypter un message chiffré par RSA, sous réserve qu’un oracle nous indique si le padding d’un cryptogramme donné est correct ou non.

Soit une paire de clés RSA 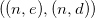, représentant respectivement le module de la clé, l’exposant publique, et l’exposant privé.

Considérons de plus un message 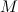, et 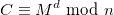le cryptogramme correspondant.

Notons 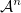l’ensemble des mots de longueur inférieure à 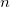de l’alphabet 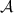contenant tous les caractères usuels, 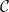l’ensemble des cryptogrammes pouvant être générés à l’aide de la clé privée 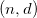, 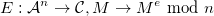la fonction de chiffrement RSA, et 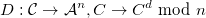la fonction de déchiffrement RSA.

L’attaquant dispose du message chiffré 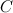, et a la possibilité de soumettre un message à un oracle qui va déchiffrer ce ciphertext, et nous informer de la validité du padding. Notons 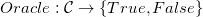la fonction permettant d’effectuer une telle requête à l’oracle.

Rappelons également une propriété du chiffrement RSA qui nous sera très utile au cours de cette attaque, en conservant les notations précédemment introduites :

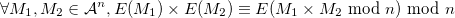
En effet, on a, :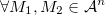

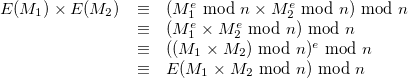
L’algorithme

L’algorithme sur lequel repose cette attaque se décompose en quatre parties :

1. Blinding

Il s’agit, dans un premier temps, de faire en sorte que l’oracle ne puisse pas prendre connaissance du cryptogramme que l’on essaye de déchiffrer. Pour ce faire, nous allons générer aléatoirement des entiers positifs 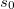jusqu’à ce que 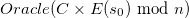nous retourne vrai, c’est-à-dire jusqu’à ce que 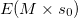soit conforme. Nous appellerons 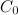le cryptogramme obtenu à l’issue de cette première étape.

Notons 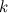la longueur en bytes de n, et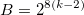

2. Searching for PKCS conforming messages

Bleichenbacher distingue alors trois cas :

Soit nous effectuons l’itération initiale de l’algorithme, et alors il s’agit de rechercher le premier 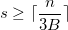tel que l’on ait 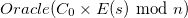, puis de poser 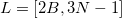, sachant que les 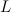seront des listes d’intervalles dont l’un encadrera le message en clair recherché ;
Soit nous effectuons une itération non-initiale, et la longueur courante de 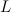est supérieure à 2, et alors nous recherchons le premier supérieur à la valeur du obtenu lors de l’itération précédente, tel que l’on ait ;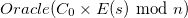
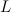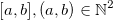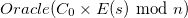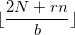Soit nous effectuons une itération non-initiale, et la longueur courante de est égale à 1. Nous avons donc un unique intervalle , si bien que l’on peut utiliser une recherche binaire optimisée afin de trouver la prochaine valeur de telle que l’ont ait . Il s’agit tester les compris entre et 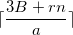, avec .

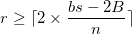3. Narrowing the set of solutions

Une fois que nous avons trouvé et que nous avons une liste d’intervalles 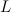, nous allons créer une nouvelle liste 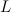contenant des intervalles plus précis, et moins nombreux dans le cas où l’on a plusieurs intervalles.

Pour ce faire, il nous faut considérer chaque intervalle 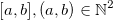contenue dans 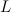, et, pour ,

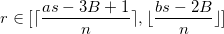Trouver le minimum 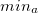entre et ;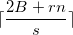
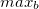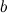Trouver le maximum entre et ;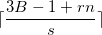
Ajouter l’intervalle 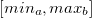à la nouvelle liste 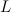que l’on est en train de former uniquement si .

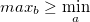Ainsi, au fur et à mesure des itérations, nous nous débarrasserons des intervalles superflues, afin d’obtenir, à terme, un unique intervalle qui pourra être affiné très rapidement grâce à la recherche binaire, jusqu’à ce que les deux bornes de celui-ci soient égales.

4. Computing the solution

Une fois la nouvelle liste obtenue, on distingue deux cas :

Soit 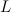est composé d’un unique encadrement 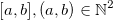d’amplitude nulle, et alors on obtient directement le message en calculant 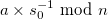, le modulo inverse de 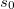pouvant être facilement calculé à l’aide de l’algorithme d’Euclide étendu ;
Soit on retourne à l’étape 2.

Pour plus de précisions, nous vous invitons à lire l’article original de Bleichenbacher.

L’implémentation

L’implémentation de cet algorithme repose sur une optimisation bien connue : l’exponentiation modulaire. En effet, dans la pratique, l’exposant peut valoir 65537, et les sont souvent composés de plus d’une quinzaine de chiffres, ce qui peut rentre le calcul de 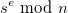particulièrement long si l’on n’applique le modulo qu’à la fin de calcul, comme nous avons pu le voir dans certaines implémentations en Python (e ** s % n). Nous avons choisi d’utiliser la fonction built-in pow, qui permet d’effectuer les calculs modulo 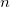, ce qui évitera de manipuler des nombres supérieurs à 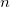lors de l’exponentiation.

Voici une démonstration de notre implémentation en Python : Attaque de Bleichenbacher (désormais intégrée à RSHack), dans le cas particulier d’un module de 2048 bits, avec un exposant publique égal à 65537, sur un unique bloc de 256 bytes. Les caractères non-imprimables affichés avant le message en clair correspondent au padding mis en place par openssl selon la norme PCKS#1 v1.5.

zweisamkeit@linux [ Bleichenbacher ] --> ncat -lvp 4444 -e ./oracle.py --keep-open 1>/dev/null 2>&1 &
zweisamkeit@linux [ Bleichenbacher ] --> openssl genrsa 2048 > private.key 2>/dev/null
zweisamkeit@linux [ Bleichenbacher ] --> openssl rsa -pubout < private.key > public.key 2>/dev/null
zweisamkeit@linux [ Bleichenbacher ] --> module=$(openssl rsa -pubin -in public.key -modulus 2>/dev/null | grep Modulus | cut -d '=' -f 2)
zweisamkeit@linux [ Bleichenbacher ] --> exposant=$(openssl rsa -in public.key -pubin -text -noout | grep Exponent | cut -d ' ' -f 2)
zweisamkeit@linux [ Bleichenbacher ] --> message=$(echo -ne "Elle t’a si tendrement serrée à la gorge que tu en as gardé pour toujours l’envie de pleurer.")
zweisamkeit@linux [ Bleichenbacher ] --> cryptogramme=$( echo -en $message | openssl rsautl -encrypt -inkey private.key | xxd -ps | tr -d '\n')
zweisamkeit@linux [ Bleichenbacher ] --> time ./bleichenbacher.py $module $exposant $cryptogramme localhost 4444 "Padding Error"


	~~~~~~~~~~~~~~~~~~~~~~~~~
	Attaque de Bleichenbacher
	       Zweisamkeit       
	    Licence GNU GPL v3   
	~~~~~~~~~~~~~~~~~~~~~~~~~


	Établissement de la connexion à l'Oracle...
	Connexion à l'Oracle établie.

	Lancement de l'attaque...

	Brouillage en cours...
	Brouillage terminé.

	Construction et affinage des encadrements en cours...
	Construction et affinage des encadrements terminés.

	Le message en clair est : 

          [Random Padding] Elle t’a si tendrement serrée à la gorge que tu en as gardé pour toujours l’envie de pleurer.
	Fin de l'attaque.

	Connexion cloturée.


real	3m11,328s
user	0m35,287s
sys	0m1,880s