Cryptanalyse du Chiffre de Vigenère

Le Chiffre de Vigenère est un algorithme de substitution poly-alphabétique dont le fonctionnement est assez proche de celui du Chiffre de César. La différence se situe dans la taille de la clé : le Chiffre de Vigenère prend également un message clair en entrée, mais, contrairement à César, la clé n’est pas nécessairement constituée d’un unique caractère, mais peut en contenir plusieurs. Le message chiffré est obtenu en appliquant un décalage circulaire sur chaque élément du plaintext, en prenant pour offset la position dans l’alphabet considéré des éléments de la clé répétée autant de fois que nécessaire.

Pour être plus clair, considérons l’alphabet latin 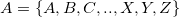, un plaintext 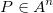, avec 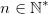, et la clé 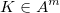, avec .

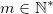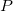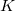et peuvent s’écrire comme la concaténation de 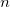éléments de :

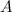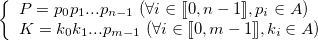
Soient 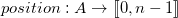une fonction renvoyant la position dans 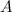du caractère passé en argument, et 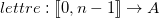la fonction réciproque.

Notons 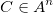le message chiffré à produire décomposé de la même manière que :

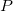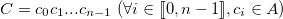
Alors on a :

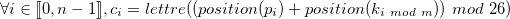
De manière analogue, pour le déchiffrement, on a :

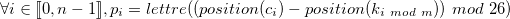
La cryptanalyse du Chiffre de Vigenère est un peu plus compliquée que celle du Chiffre de César.

Dans un premier temps, il s’agit de trouver le taille de la clé 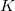, notée 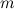au début de l’article, et inconnue dans notre situation.

Pour cela, introduisons la notion d’indice de coïncidence, noté 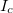, en considérant que, 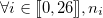correspond au nombre de répétitions de la lettre 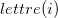dans :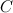

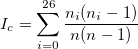
Cet indice correspond à la probabilité que deux éléments d’un texte donné tirés aléatoirement soient identiques. Chaque langue a un indice de coïncidence spécifique. Notons 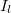l’indice de coïncidence de la langue utilisée.

Par la suite, on utilise le Test de Friedman :

On décompose le cryptogramme en 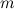listes de sous-cryptogrammes, que nous noterons :

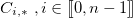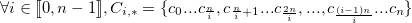
Et on note :

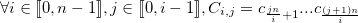
Pour chaque liste, on calcule l’indice de coïncidence des différents sous-cryptogrammes qui la composent, puis on calcule la moyenne de ces indices, notée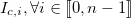

L’indice le plus proche de l’indice de référence indiquera la longueur de clé la plus probable :

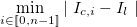
Une fois la taille de la clé connue, il suffit de décomposer le cryptogramme en 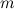sous-cryptogrammes de la manière suivante :

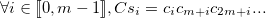
Sur chacun de ces sous-cryptogrammes, on effectue une analyse fréquentielle relative à la langue utilisée afin de déterminer le décalage « local », nous permettant ainsi de recomposer le sous-plaintext correspondant, ainsi que nous l’avons fait pour le Chiffre de César.

Enfin, il suffit de reconstituer 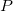à partir des sous-plaintext obtenus.

Voici une implémentation en C de cette méthode ce cryptanalyse : Cryptanalyse du Chiffre de Vigenère

zweisamkeit@linux [ Vigenere ] --> ./decrypt_vigenere ciphertext plaintext fr


		~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

		Cryptanalysis of the Chiffre de Vigenère

		           Zweisamkeit -- 2016

		             License GNU/GPL

		~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Probable length of the key : 5

Probable key  : RILKE

zweisamkeit@linux [ Vigenere ] --> cat plaintext 
Dites vos tristesses et vos désirs, les pensées qui vous viennent,
votre foi en une beauté. Dites tout cela avec une sincérité intime,
tranquille et humble. Utilisez pour vous exprimer les choses qui
vous entourent, les images de vos songes, les objets de vos souvenirs.
Si votre quotidien vous paraît pauvre, ne l’accusez pas. Accusez-vous
vous-même de ne pas être assez poète pour appeler à vous ses richesses.
Pour le créateur rien n’est pauvre, il n’est pas de lieux pauvres,
indifférents. Même si vous étiez dans une prison, dont les murs
étoufferaient tous les bruits du monde, ne vous resterait-il pas
toujours votre enfance, cette précieuse, cette royale richesse,
ce trésor des souvenirs ?

- Lettres à un jeune poète, Rainer Maria Rilke